Algoritmo della linea di Bresenham

L'algoritmo della linea di Bresenham (da alcuni chiamato algoritmo del punto medio o anche Cerchi di Bresenham) è un algoritmo di rasterizzazione di linea. Allo stato attuale è l'algoritmo più usato per la rasterizzazione di linee, soprattutto per la sua bassa richiesta di risorse computazionali.

Descrizione

Per capire l'algoritmo, semplifichiamo il problema assumendo che ${\displaystyle m={\frac {\Delta y}{\Delta x}}}$ sia compreso tra ${\displaystyle 0$.

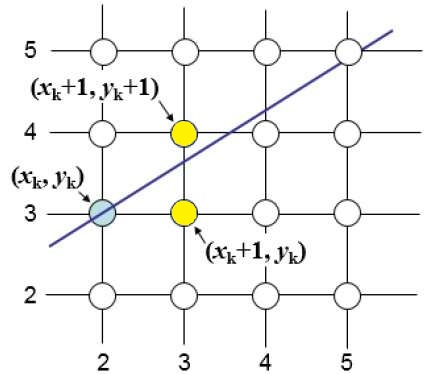
Immaginiamo di trovarci ad un passo ${\displaystyle i}$ dell'algoritmo, cioè abbiamo appena determinato quale pixel "accendere", per esempio ${\displaystyle p_{1}(x_{1},y_{1})}$.

Ora dobbiamo determinare il prossimo pixel da "accendere", chiamiamolo ${\displaystyle p_{2}(x_{2},y_{2})}$, dove ${\displaystyle x_{2}=x_{1} 1}$.

La situazione è quella riportata in figura 1, dove dal punto 1 (quello in verde) dobbiamo passare al punto 2 che si può trovare subito a destra, caso A, o in alto a destra, caso B.

• Nel caso A abbiamo ${\displaystyle y_{2}=y_{1}}$;
• Nel caso B abbiamo ${\displaystyle y_{2}=y_{1} 1}$.

Prendiamo in considerazione il punto ${\displaystyle M(x_{1} 1,y_{1} {1 \over 2})}$ (Figura 2), punto medio tra A e B. Se la linea da rasterizzare passa sopra, illumineremo il pixel superiore B, altrimenti il pixel inferiore A.

Per determinare se ${\displaystyle M}$ si trova sotto o sopra la retta, consideriamo la forma esplicita dell'equazione della retta:

${\displaystyle y={\frac {\Delta y}{\Delta x}}\cdot x q}$

che può essere riscritta nella forma:

${\displaystyle -\Delta x\cdot y \Delta y\cdot x \Delta x\cdot q=0}$

Tutti i punti appartenenti alla retta devono verificare l'equazione. Ma questa retta divide anche due semipiani, quello composto da tutti i punti per cui la formula precedente restituisce un valore positivo e quello per cui restituisce un valore negativo. Un esempio dei semipiani lo troviamo nella figura 3.

Quindi dalla formula precedente possiamo ricavare il valore decisionale ${\displaystyle d}$, sostituendo ad ${\displaystyle x}$ ed ${\displaystyle y}$ le coordinate di ${\displaystyle M(x_{1} 1,y_{1} 1/2)}$ (il punto medio tra A e B):

${\displaystyle d=-\Delta x\cdot y_{M} \Delta y\cdot x_{M} \Delta x\cdot q}$

il quale sarà:

• ${\displaystyle d=0}$, se il punto giace sulla retta; in questo caso possiamo scegliere in modo indifferente il punto A o il punto B;
• ${\displaystyle d<0}$, se il punto si trova sopra la retta; in questo caso prendiamo il punto A;
• ${\displaystyle d>0}$, se il punto si trova sotto la retta; in questo caso prendiamo il punto B.

Nell'algoritmo avremmo necessità ogni volta di sapere se ${\displaystyle d}$ è positivo o negativo.

Ipotizziamo di aver scelto il punto A, in questo caso il nostro punto di partenza ${\displaystyle p}$ è ${\displaystyle p(x_{1} 1,y_{1})}$, e il nostro nuovo punto medio M è ${\displaystyle M(x_{1} 2,y_{1} {1 \over 2})}$. Invece il nuovo valore di ${\displaystyle d}$ è:

${\displaystyle d_{new}=-\Delta x\cdot y_{M} \Delta y\cdot x_{M} \Delta x\cdot q=-\Delta x\cdot \left(y_{1} {\frac {1}{2}}\right) \Delta y\cdot (x_{1} 2) \Delta x\cdot q}$

Proviamo a sottrarre al nuovo valore di ${\displaystyle d}$ quello vecchio:

${\displaystyle d_{new}-d_{old}=-\Delta x\cdot \left(y_{1} {\frac {1}{2}}\right) \Delta y\cdot (x_{1} 2) \Delta x\cdot q-\left(-\Delta x\cdot \left(y_{1} {\frac {1}{2}}\right) \Delta y\cdot (x_{1} 1) \Delta x\cdot q\right)}$

Semplificando otteniamo:

${\displaystyle d_{new}-d_{old}=\Delta y}$

Quindi abbiamo modo di ricavare il nuovo valore ${\displaystyle d}$ in modo più semplice dal vecchio, senza ogni volta rifare tutti i calcoli.

Ora dobbiamo fare l'ipotesi per il caso in cui si sia scelto il punto B. Abbiamo i nostri nuovi punti:

• ${\displaystyle p(x_{1} 1,y_{1} 1)}$;
• ${\displaystyle M(x_{1} 2,y_{1} 1 {1 \over 2})=M(x_{1} 2,y_{1} {3 \over 2})}$;

e il nostro nuovo valore ${\displaystyle d}$:

${\displaystyle d_{new}=-\Delta x\cdot \left(y_{1} {\frac {3}{2}}\right) \Delta y\cdot (x_{1} 2) \Delta x\cdot q}$

Ripetiamo la sottrazione:

${\displaystyle d_{new}-d_{old}=-\Delta x\cdot \left(y_{1} {\frac {3}{2}}\right) \Delta y\cdot (x_{1} 2) \Delta x\cdot q-\left(-\Delta x\cdot \left(y_{1} {\frac {1}{2}}\right) \Delta y\cdot (x_{1} 1) \Delta x\cdot q\right)}$

Semplificando otteniamo:

${\displaystyle d_{new}-d_{old}=-\Delta x \Delta y}$

Riassumendo, dato un valore ${\displaystyle d_{i}}$:

${\displaystyle d_{i 1}=\left\{{\begin{matrix}d_{i}-\Delta x \Delta y,&{\mbox{se }}d_{i}>0\\d_{i} \Delta y,&{\mbox{se }}d_{i}<0\end{matrix}}\right.}$

Non ci rimane che conoscere il valore ${\displaystyle d_{0}}$; ricordandoci la formula per calcolare ${\displaystyle d}$ e prendendo come punto ${\displaystyle p}$, ${\displaystyle p_{0}(x_{0},y_{0})}$ ovvero un estremo della retta, abbiamo:

${\displaystyle d=-\Delta x\cdot \left(y_{0} {\frac {1}{2}}\right) \Delta y\cdot (x_{0} 1) \Delta x\cdot q=-\Delta x\cdot y_{0} \Delta y\cdot x_{0} \Delta x\cdot q \left(-{\frac {\Delta x}{2}} \Delta y\right)}$

Nel passaggio abbiamo portato fuori i valori ${\displaystyle 1/2}$ e ${\displaystyle 1}$. La prima parte della formula corrisponde all'equazione della retta applicata ad un punto della retta, quindi sappiamo che sarà uguale a zero. Infine ci rimane:

${\displaystyle d_{0}=-{\frac {\Delta x}{2}} \Delta y}$

Algoritmo

Da tutte queste formule possiamo finalmente ricavare l'algoritmo: Dati due punti ${\displaystyle p_{1}}$ e ${\displaystyle p_{2}}$, con coordinate (x₁,y₁) e (x₂,y₂):

DX = x2 - x1
DY = y2 - y1

//il nostro valore d0
d = - 1/2 * DX   DY

//assegna le coordinate iniziali
x = x1
y = y1
disegna_il_punto(x, y)

while x < x2 {
       if (d >= 0) {
        d = d -DX   DY;
        y = y   1;
        x = x   1;
       }
       else {
        d = d   DY;
        x = x   1;
       }
       disegna_il_punto(x, y)
}

Notiamo che l'algoritmo presenta dei numeri in virgola mobile, i quali richiedono risorse computazionali, un'idea per evitare questa precisione è quella di raddoppiare i valori di ${\displaystyle d}$:

DX = x2 - x1
DY = y2 - y1

//il nostro valore d0
d = - DX   2 * DY

//assegna le coordinate iniziali
x = x1
y = y1
disegna_il_punto(x, y)

while x < x2 {
       if (d >= 0) {
        d = d -2 * DX   2 * DY;
        y = y   1;
        x = x   1;
       }
       else {
        d = d   2 * DY;
        x = x   1;
       }
       disegna_il_punto(x, y)
}

Abbiamo quindi ottenuto un algoritmo che lavora con numeri interi e semplice da implementare. Nel caso in cui avessimo x₁>x₂ allora al posto di aumentare ${\displaystyle x}$ lo diminuiamo mentre i valori decisionali restano uguali, anche se y₁>y₂ i valori decisionali non variano, in quanto la retta assume pendenza di valore opposto a quello del caso y₁2 e x₁2, cambia solo l'incremento della ${\displaystyle y}$ che invece di aumentare, diminuisce, e il valore decisionale resta invariato, in quanto trattiamo la retta sia se x₁>x₂ sia se y₁>y₂ come se fosse nel primo caso studiato, nel primo caso sia DX che DY sono maggiori di zero allora prenderemo il valore assoluto, di seguito ricaviamo l'algoritmo:

DX = x2 - x1
DY = y2 - y1

//per non scrivere sempre i valori assoluti cambio DY e DX con altre variabili
a=abs(DY)
b=-abs(DX)

//il nostro valore d0
d = 2*a b
//assegna le coordinate iniziali
x = x1
y = y1
disegna_il_punto(x, y)

//s e q sono gli incrementi di x e y
s=1
q=1
if (x1>x2) q=-1
if (y1>y2) s=-1

while x < x2 {
       if (d >= 0) {
        d = 2 * (a   b)   d
        y = y   s;
        x = x   q;
       }
       else {
        d = 2 * a   d;
        x = x   q;
       }
       disegna_il_punto(x, y)
}

Con questo abbiamo ottenuto le rette con valore di ${\displaystyle |m|<1}$. Con valore di ${\displaystyle |m|>1}$ dobbiamo fare delle modifiche perché |DY/DX|>1 e questo accade quando DY>DX in questo caso l'approssimazione della linea con l'algoritmo che abbiamo trovato è pessima, visto che viene trattato solo DX come loop, dobbiamo generalizzare l'algoritmo nei casi in cui possiamo avere DY>DX. Se ruotiamo la retta di 90 gradi possiamo notare che è come se dovessimo applicare lo stesso algoritmo precedente con la coordinata dei due punti da scegliere x invece che ${\displaystyle y}$, allora in questo caso trattiamo DY come DX e DY come DX, basta quindi scambiare DX e DY e rimanere i valori decisionali invariati, nel loop possiamo avere DX>DY oppure DY>DX ma siccome scambiamo sarà sempre DX>DY, poi nel caso in cui d>=0 avremo che entrambe le coordinate aumentano o diminuiscono di 1, quindi questo caso rimane uguale, cambia invece il caso in cui ${\displaystyle d<0}$ in questo caso infatti dobbiamo decidere se aumentare solo ${\displaystyle x}$ o solo ${\displaystyle y}$ in base al caso che abbiamo. Nel caso normale si aumenta ${\displaystyle x}$, nel caso DY>DX si scambiano e si aumenta ${\displaystyle y}$, da questa logica possiamo ricavare l'algoritmo per linee generali che è il seguente:

swap = 0;
DX = x2 - x1;
DY = y2 - y1;

//siccome scambio DY e DX ho sempre DX>=DY allora per sapere quale coordinata occorre cambiare uso una variabile
if (abs(DX) < abs(DY)) {
   swap(DX, DY);
   swap = 1;
}

//per non scrivere sempre i valori assoluti cambio DY e DX con altre variabili
a = abs(DY);
b = -abs(DX);

//assegna le coordinate iniziali
x = x1;
y = y1;

//il nostro valore d0
d = 2 * a   b;

//s e q sono gli incrementi/decrementi di x e y
q = 1;
s = 1;
if (x1 > x2) q = -1;
if (y1 > y2) s = -1;
disegna_punto(x, y);
disegna_punto(x2, y2);
for (k = 0; k < -b; k =1) {
   if (d > 0) {
       x= x   q; y= y   s;
       d= d   2 * (a   b);
   }
   else {
       x = x   q;
       if (swap==1) { y = y   s; x = x - q; }
       d = d   2 * a;
   }
   disegna_punto(x, y);
}

Altri progetti

• Wikimedia Commons contiene immagini o altri file sull'algoritmo della linea di Bresenham

Collegamenti esterni

• (EN) Eric W. Weisstein, Bresenham's Line Algorithm, su MathWorld, Wolfram Research.