Processo di Lévy

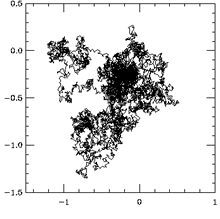
In teoria della probabilità, un processo di Lévy (dal matematico francese Paul Lévy) è un processo stocastico con incrementi stazionari e indipendenti: rappresenta il moto di un punto i cui movimenti successivi siano indipendenti e siano identicamente distribuiti su intervalli di tempo della stessa lunghezza. Può essere visto come una versione continua della passeggiata aleatoria.

I processi di Levy più conosciuti sono il processo di Poisson e il moto browniano. Tutti i processi di Lévy sono anche processi additivi.

Definizione

Un processo stocastico ${\displaystyle X=\{X_{t}:t\geq 0\}}$ è detto processo di Lévy se:

• ${\displaystyle X_{0}=0}$ quasi certamente.
• Ha incrementi indipendenti, ovvero per ogni scelta di tempi ${\displaystyle 0\leq t_{1}<\cdots$, le variabili aleatorie ${\displaystyle X_{t_{2}}-X_{t_{1}},X_{t_{3}}-X_{t_{2}},\dots ,X_{t_{n}}-X_{t_{n-1}}}$ sono indipendenti.
• Ha incrementi stazionari, ovvero per ogni scelta di ${\displaystyle s$, la variabile aleatoria ${\displaystyle X_{t}-X_{s}}$ ha la stessa legge di ${\displaystyle X_{t-s}}$.

Proprietà

• Ogni processo di Lévy possiede una versione càdlàg quasi certamente.